2019ICCV Gaze360: Physically Unconstrained Gaze Estimation in the Wild
abstract
了解人们在看什么是一个信息丰富的社会线索。在这项工作中,介绍了Gaze360,这是一个大规模的凝视跟踪数据集,以及在无约束图像中进行鲁棒3D凝视估计的方法。
数据集包括室内和室外环境中的238名受试者,他们在各种头部姿势和距离上进行标记的3D凝视。这是通过一种简单而高效的收集方法,从主题和种类来看,它是同类数据中最大的公开可用数据集。
提出的3D凝视模型扩展了现有模型,包括时间信息,并直接输出凝视不确定性的估计。
消融研究展示了模型的优点,并通过与其他近期基准数据集的交叉数据集评估展示了其泛化性能。此外,文章还提出了一种简单的自监督方法来改进跨数据集域自适应。最后展示了我们的模型在超市环境中估计顾客注意力的应用。
数据集和模型在http://gaze360.csail.mit.edu。
introduction
近年来,虽然通过利用深度卷积神经网络的代表能力以及非常大的注释数据集[2,6,9,14,26],2D身体姿势和面部跟踪等相关人体建模问题的方法取得了令人印象深刻的成功,但凝视估计方法尚未达到这样的性能水平。这主要是因为缺乏足够大且多样的任务注释训练数据。利用地面真实信息收集精确且高度多样的凝视数据,尤其是在实验室之外,是一项具有挑战性的任务。
在这项工作中,引入了一种方法来帮助解决这项任务,并缩小感知的绩效差距:
首先描述了一种在任意环境中有效收集带注释的3D凝视数据的方法;
使用我们的方法获得最大的3D凝视,文献中的数据集按主题和种类分类,在室内和室外条件下拍摄了238名受试者的视频,我们仔细评估了数据集的误差和特点,
- 在数据集上训练各种3D凝视估计模型,然后收敛到最终模型,该模型唯一地接受多帧输入(以帮助解决单帧模糊性),并使用 pinball回归损失进行误差分位数回归,以提供凝视不确定性的估计;
- 通过跨数据集模型性能比较(在一个数据集上进行训练,在另一个数据集上进行测试)证明了我们的数据集与现有数据集的有效性,并介绍了一种简单的凝视模型自监督域自适应方法;
- 最后,演示如何将Gaze360模型应用于现实世界的用例,例如估计超市中顾客的注意力。
Gaze360 model
视线是一种自然持续的信号。视线的固定和转换会产生一系列视线。为了利用这一点,我们提出了一种基于视频的凝视跟踪模型使用双向长短时记忆胶囊(LSTM)[5],它提供了一种建模序列的方法,其中一个元素的输出取决于过去和未来的输入。在本文中,利用7帧序列来预测中心帧的注视。请注意,其他序列长度(包括单个中心帧)也是可能的。
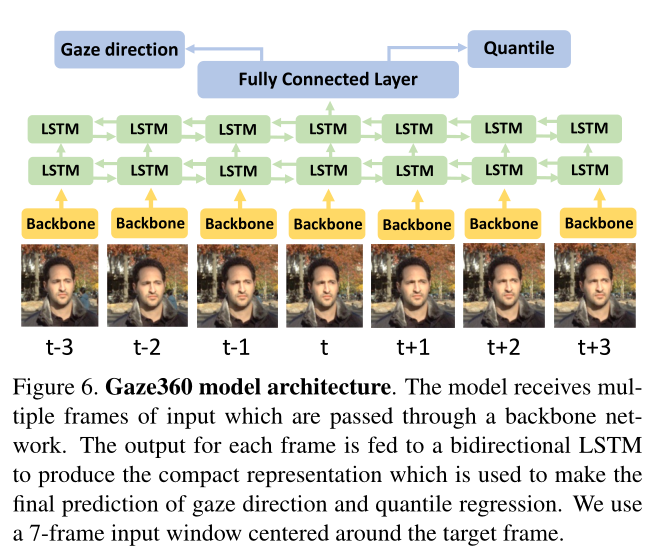
该模型接收多个输入帧,这些帧通过主干网传输。每一帧的输出被馈送到一个双向LSTM以产生紧凑的表示,该表示用于对注视方向和分位数回归进行最终预测。使用以目标帧为中心的7帧作为输入窗口。
图6示出了Gaze360模型的架构。来自每一帧的头部裁剪由卷积神经网络(主干)单独处理,该网络产生维度256的高级特征。这些特征被馈送到具有两层的双向LSTM,这两层在向前和向后向量中分解序列。最后,这些向量被连接并通过一个完全连接的层来产生两个输出:注视预测和误差分位数估计。
使用ImageNet预训练的ResNet-18[7]作为骨干网络。所有模型都使用Adam optimizer[13]在Pytorch中进行了训练,学习率为10−4.
5.1误差分位数估计
分位数(quantile) - ParamousGIS - 博客园 (cnblogs.com)
据我们所知,所有现有的将神经网络应用于注视估计任务的研究都没有考虑误差范围。在不受约束的环境中估算凝视时,误差范围是有用的,因为当眼睛从侧面看时,或者当一只或多只眼睛部分被遮挡时,精度可能会降低。在分类设置中,softmax输出经常被用作置信度的代理。然而,对于回归来说,这是不可能的,因为输出的大小直接对应于预测的属性。
为了建模误差界限,我们使用pinball损失函数[15]来预测误差分位数。我们使用一个单一的网络来预测平均值以及10%和90%分位数。
这样做的结果是,对于给定的图像,我们通过一次向前传递估计出预期的注视方向和一个误差范围,在80%的时间里,gt都在这个范围内。
zff 80%的时间里, 次数?
我们假设在球坐标系中分布是各向同性的。这个假设严格来说是不正确的,特别是对于由于极点奇点周围的空间扭曲而产生的大俯仰角然而,对于大多数观测到的注视方向(图4)来说,这是一个合理的近似,可以降低维度,简化结果的解释。
我们的网络是的输出$f(I) =(θ,φ,σ)$,在$(θ,φ)$是预期的yaw和pitch。第三个参数σ对应于预期凝视的偏移,θ + σ和φ + σ是它们分布的90%分位数,而θ - σ和φ - σ是10%分位数。
最后,我们计算这个输出的pinball损失。这自然会迫使φ和θ收敛于它们的地真值,σ收敛于分位数阈值。如果$y = (θ_{gt}, φ_{gt})$,分位数τ和角度θ的损失Lτ可表示为:
我们将角度和分位数τ = 0.1和τ = 0.9的损失都取平均值。σ是10%和90%分位数与期望值之间差异的度量.